An analogy between metabolism and electricity suggests that the “law of diminishing returns” applies to metabolic networks of any complexity
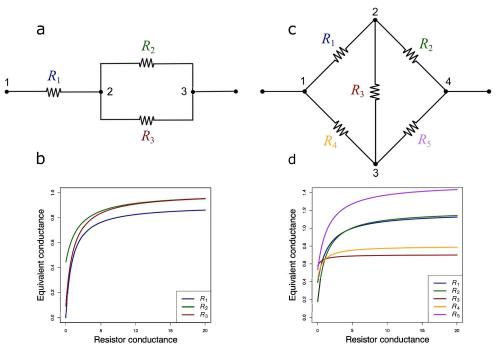
In economics, the ‘law of diminishing returns’ tells us that the gain in production resulting from the gradual increase in a factor of production becomes smaller and smaller as that factor increases. The same phenomenon is often observed in biology: when the concentration or activity of a cellular component increases, the effect on the phenotype is initially high, then gradually fades and finally reaches a plateau. For instance, if the concentration of an enzyme in a metabolic pathway increases from a low value, the metabolic flux through this pathway increases rapidly at first, then less and less as the enzyme concentration becomes higher. Is this type of concave response with asymptote valid for metabolic networks of any complexity, whose topology could induce different types of response?
To address this question, M. Petrizzelli, C. Coton and D. de Vienne (IDEEV, GQE–Le Moulon, Université Paris-Saclay) used mathematical developments initially designed to model currents in electrical circuits. This approach is justified by the fact that matter and/or energy exchange networks (in biochemistry, electricity, mechanics, hydraulics, thermodynamics, etc.) share common properties that can be described by similar equations. Thus, the authors showed that the law of diminishing returns applies to metabolic networks whatever their topology (Figure 1). This result was formally demonstrated for networks including uni-uni reactions (A⇌B), and indirect arguments suggest that this is also the case when networks include bi-bi reactions (A+B⇌P+Q).
This generalisation helps to shed light on the origin of the concave relationships that are frequently observed between different levels of organisation, relationships that can explain, in particular, the dominance of the most active alleles over less active ones, the hybrid vigor and the epistasis.
Read the article :
Contact : Dominique de Vienne