Combinant mathématiques, génétique in vitro et simulations, et en s’appuyant sur une analyse bibliographique approfondie, des chercheurs du Moulon et de Montpellier proposent une explication générale du phénomène d’hétérosis.
Lorsqu’on croise deux individus génétiquement éloignés, il est fréquent que leur descendance montre une « vigueur » supérieure à celle de ses parents : la croissance est plus rapide, l’âge de la reproduction plus précoce, la fertilité plus élevée, la résistance aux maladies meilleure, etc. Ce phénomène universel, appelé hétérosis, est exploité empiriquement depuis des millénaires (cf. le mulet), et fait l’objet de nombreux travaux depuis le début du XXe siècle dans le cadre de son utilisation en sélection animale et végétale. Même s’il a été expliqué au niveau moléculaire dans quelques cas, l’hétérosis reste souvent qualifié de « mystérieux », d’« insaisissable », voire de « magique », en raison notamment de son ampleur, qui peut être spectaculaire : les maïs hybrides peuvent avoir un rendement double de celui de parents, et la vitesse de croissance de certaines souches hybrides de levure excède celle des souches parentales de plus d’un ordre de grandeur.
Une équipe de l’UMR GQE – Le Moulon, en collaboration avec le laboratoire Sciences pour l’œnologie de l’INRA de Montpellier, a montré qu’une approche systémique de ce phénomène permettait d’en donner une explication générale. La clé de l’énigme réside en ce qu’on appelle en économie la « loi des rendements décroissants » : lorsque la concentration ou l’activité d’un constituant cellulaire augmente progressivement, l’effet sur le phénotype est d’abord élevé, puis s’estompe petit à petit pour finalement plafonner. Par exemple si la concentration d’une enzyme d’un réseau métabolique augmente à partir d’une valeur faible, le flux métabolique à travers ce réseau croît d’abord rapidement, puis de moins en moins à mesure que la concentration de l’enzyme devient élevée. Ce type de comportement, qui a été décrit à différents niveaux d’organisation, de la transcription/traduction à la valeur sélective, rend compte de la dominance très fréquente des allèles les plus actifs sur les moins actifs (figure 1A). Si l’on considère conjointement deux ou plusieurs constituants, l’hétérosis émerge du système en tant que généralisation de la dominance. En effet, comme on le voit figure 1B, la courbure de la surface décrivant la relation entre le génotype et le phénotype fait que la valeur phénotypique de l’hybride dépasse celle de la moyenne de ses parents, voire dans certains cas celle du meilleur parent. Ce modèle d’hétérosis a été formalisé mathématiquement grâce à la théorie des fonctions concaves, puis validé à la fois expérimentalement par génétique in vitro et informatiquement grâce à des simulations de la glycolyse de levure. Cette vision de l’hétérosis ouvre la voie à de nouveaux critères de prédiction du phénomène.
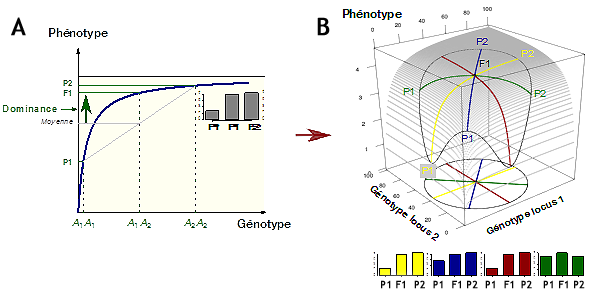
fig1 : Relation génotype-phénotype et hérédité
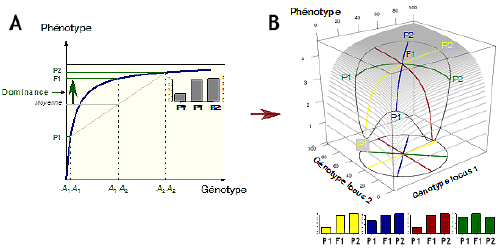
Figure 1.
- A. Aux trois génotypes A1A1, A1A2 et A2A2 correspondent les valeurs phénotypiques P1, F1 et P2, respectivement. La courbure de la relation fait que la valeur de l’hybride F1 est supérieure à la celle de la moyenne des valeurs parentales (voir vignette) : il y a dominance de l’allèle A2 sur l’allèle A1.
- B. Avec deux locus variables, la relation génotype-phénotype forme une surface concave. Quatre paires de parents sont ici représentées dans le plan des génotypes, aux extrémités des diamètres jaune, bleu rouge et vert d’un cercle centré sur une même valeur génotypique de l’hybride. Les valeurs phénotypiques résultantes sont visibles sur la surface. Dans tous les cas il y a de l’hétérosis, dont l’ampleur dépend de la position des parents dans le plan des génotypes (voir les quatre diagrammes sous la figure).
Référence
Contacts : Julie Fiévet et Dominique de Vienne